Trägheitsnavigation: Unterschied zwischen den Versionen
K (→Rotationen) |
K (→Rotationen) |
||
| Zeile 40: | Zeile 40: | ||
Aus einer 3-achsigen Drehgeschwindigkeit vrot in rad/s und einer Zeitspanne delta_t in Sekunden lässt sich ein 3-achsiger Rotationswinkel über a=vrot*delta_t in rad bestimmen. Die drei Winkel ax, ay und az lassen sich per [http://de.wikipedia.org/wiki/Rodrigues-Formel Rodrigues-Formel] in eine Rotationsmatrix umwandeln. Allerdings erfordert die Auswertung dieser Formel eine Wurzel für die 2-Norm ||a|| von a sowie die Berechnung von sin(||a||) und cos(||a||). | Aus einer 3-achsigen Drehgeschwindigkeit vrot in rad/s und einer Zeitspanne delta_t in Sekunden lässt sich ein 3-achsiger Rotationswinkel über a=vrot*delta_t in rad bestimmen. Die drei Winkel ax, ay und az lassen sich per [http://de.wikipedia.org/wiki/Rodrigues-Formel Rodrigues-Formel] in eine Rotationsmatrix umwandeln. Allerdings erfordert die Auswertung dieser Formel eine Wurzel für die 2-Norm ||a|| von a sowie die Berechnung von sin(||a||) und cos(||a||). | ||
Für sehr kleine Drehwinkel könnte man eine Linearisierung verwenden: | Für sehr kleine Drehwinkel könnte man eine Linearisierung verwenden: | ||
| Zeile 50: | Zeile 48: | ||
Hier kommt man ohne komplizierte Funktionen wie sqrt, sin und cos aus. Die eckigen Klammern machen aus einem Vektor eine Matrix. Man beachte aber, dass das hier bei a!=0 keine Rotationsmatrix mehr ist und dass man wenn man die von rechts an die aktuelle Orientierungsmatrix dranmultipliziert letztere wieder "normalisieren" muss. Das geht über ein paar Kreuzprodukte sowie Skalierungen. Für das Normalisieren von Zeilen oder Spalten auf 1 kommt man auch um die Wurzel herum, wenn man 1/sqrt(t) mit 1.5-0.5*t approximiert. So eine Normalisierung muss man so oder so durchführen, weil sich ja auch Rundungsfehler akkumulieren. | Hier kommt man ohne komplizierte Funktionen wie sqrt, sin und cos aus. Die eckigen Klammern machen aus einem Vektor eine Matrix. Man beachte aber, dass das hier bei a!=0 keine Rotationsmatrix mehr ist und dass man wenn man die von rechts an die aktuelle Orientierungsmatrix dranmultipliziert letztere wieder "normalisieren" muss. Das geht über ein paar Kreuzprodukte sowie Skalierungen. Für das Normalisieren von Zeilen oder Spalten auf 1 kommt man auch um die Wurzel herum, wenn man 1/sqrt(t) mit 1.5-0.5*t approximiert. So eine Normalisierung muss man so oder so durchführen, weil sich ja auch Rundungsfehler akkumulieren. | ||
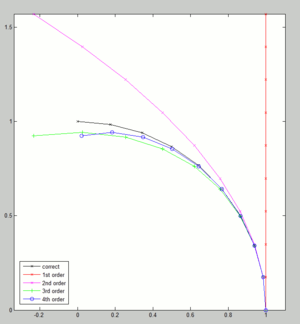
[[Datei:Rotation_approx.png|300px|thumb|right|Visualisierung der Approximationen für Rotationen, 0-90° in Schritten von 10°]] | |||
Bessere Approximationen sind immer noch ohne schwierige mathematische Funktionen möglich. Die folgende Formel entspricht einer Annäherung zweiter Ordnung: | Bessere Approximationen sind immer noch ohne schwierige mathematische Funktionen möglich. Die folgende Formel entspricht einer Annäherung zweiter Ordnung: | ||
Version vom 26. Januar 2013, 10:40 Uhr
Bei der Trägheitsnavigation kommen Inertialsensoren zum Einsatz, die auf Basis der Massenträgheit drei zueinander orthogonale translatorische und drei rotatorische Anteile einer Objektbewegung messen, um auf die Bewegung zurückzuschließen. Wie gut das mit günstigen Sensoren funktioniert, wie sie in modernen Handys verbaut sind oder zum Beispiel auf dem STM32 F3 Discovery Dev-Board zu finden sind, gilt heraus zu finden.
Gyroskop
liefert Orientierung(?) oder Drehgeschwindigkeit je nach Sensortyp(?). Die kleinen MEMS Gyroskope geben uns die Drehgeschwindigkeit.
Interessante Links dazu:
Beschleunigungssensoren
liefern Beschleunigungen. Aufgrund der Erdanziehung ist typischerweise zu erwarten, dass der gemessene Beschleunigungsvector die Summe aus tatsächlicher Beschleunigung und 1g nach oben ist. Dazu kommen dann natürlich noch Messfehler und systematische Fehler.
Probleme
- Messdaten sind verrauscht und haben einen Bias. Stärke des Rauschens und der Bias selbst sind auch Temperaturabhängig. Wie man das so mitbekommt, sind gerade MEMS Gyroskope stark temperaturabhängig, warum man auch in einigen Chips ein Thermometer integriert ist.
- Integration in Kombination mit Messrauschen ist "fies", sehe Abschnitt "Integration als Filter begreifen".
Integration als Filter begreifen
Wir kommen über Integration von Beschleunigung auf Geschwindigkeit und von Geschwindigkeit auf Position im Falle von Accelerometern. Bei Gyroskopen messen wir die Drehgeschwindigkeit und können per Integration die Orientierung bestimmen. Man kann dabei einen Integrator als Filter verstehen, der tiefe Frequenzen verstärkt und hohe Frequenzen dämpft. Genauer gesagt gibt es bei der Integration über die Zeit in Sekunden eine Amplitudenübertragung von 1/(2*pi*f), wobei f die Frequenz in Hz ist, und eine Phasenverschiebung von -90°. Dieses Filter arbeitet natürlich auch auf dem Messrauschen, weswegen die tieffrequenten Anteile (einschließlich eines Fehler-Offsets) leider kaum zu gebrauchen sind. Der aufmerksame Leser wird gemerkt haben, dass der DC-Offsent wegen 1/f sich unendlich verstärkt ... also mit der Zeit davon läuft. In IIR-Filter-Sprech ist das Ding "unstabil".
Herstellerangaben zur Genauigkeit
In den Datenblättern der Sensoren findet sich so das eine oder andere Interessante. Beispielsweise Angaben zum Rauschverhalten. Diese können da in X pro Wurzel-Hertz stehen, wobei X eine Einheit der Messgröße ist, z.B. Grad pro Sekunde für einen Gyro oder Milli-G für ein Beschleunigungsmesser. Bei dieser Angabe handelt es sich um die Wurzel der spektrale Leistungsdichte des Rauschens. Diese Angabe sagt einem den RMS-Wert des Rauschens bei einer Bandbreite von einem Hertz. Aber dieser Wert skaliert eben nur mit der Wurzel der Bandbreite. Man erhält also den 10fachen RMS-Wert bei einem Frequenzband von 100 Hz -- unter der Annahme, dass die Leistungsdichte im Spektrum konstant ist.
Eine andere Angabe, die man bei Gyros findet, ist auch der ARW, angular random walk. Der Wird bei Gyros in Grad pro Wurzel-Stunde angegeben. Er sagt einem die Rausch-induzierte Streuung in Grad, wenn man das Signal eine Stunde lang integriert. Mit dieser Angabe kann man eher etwas anfangen; denn er sagt einem gleich, welche Genauigkeit in Grad man nach Integration von einer Stunde hat. Dieser Wert skaliert auch mit der Wurzel der Zahl der Stunden.
Was noch so nützlich sein könnte
- Kalman Filter
- Complementary Filter
Programmcode/Algorithmen
- sg hat was gebastelt, ist aber noch relativ experimentell.
Rotationen
Aus einer 3-achsigen Drehgeschwindigkeit vrot in rad/s und einer Zeitspanne delta_t in Sekunden lässt sich ein 3-achsiger Rotationswinkel über a=vrot*delta_t in rad bestimmen. Die drei Winkel ax, ay und az lassen sich per Rodrigues-Formel in eine Rotationsmatrix umwandeln. Allerdings erfordert die Auswertung dieser Formel eine Wurzel für die 2-Norm ||a|| von a sowie die Berechnung von sin(||a||) und cos(||a||).
Für sehr kleine Drehwinkel könnte man eine Linearisierung verwenden:
| 0 -az ay |
R1 = I + [a] = I + | az 0 -ax | (Annäherung 1. Ordnung)
| -ay ax 0 |
Hier kommt man ohne komplizierte Funktionen wie sqrt, sin und cos aus. Die eckigen Klammern machen aus einem Vektor eine Matrix. Man beachte aber, dass das hier bei a!=0 keine Rotationsmatrix mehr ist und dass man wenn man die von rechts an die aktuelle Orientierungsmatrix dranmultipliziert letztere wieder "normalisieren" muss. Das geht über ein paar Kreuzprodukte sowie Skalierungen. Für das Normalisieren von Zeilen oder Spalten auf 1 kommt man auch um die Wurzel herum, wenn man 1/sqrt(t) mit 1.5-0.5*t approximiert. So eine Normalisierung muss man so oder so durchführen, weil sich ja auch Rundungsfehler akkumulieren.
Bessere Approximationen sind immer noch ohne schwierige mathematische Funktionen möglich. Die folgende Formel entspricht einer Annäherung zweiter Ordnung:
| -ay*ay-az*az ax*ay ax*az |
R2 = I + [a] + 1/2 * [a]^2 = R1 + 1/2 * | ax*ay -ax*ax-az*az ay*az |
| ax*az ay*az -ax*ax-ay*ay |
Die nächstbesseren Approximationen (3. und 4. Ordnung) ergeben sich mit
a2 = ||a||^2 = ax*ax+ay*ay+az*az R3 = I + (1-a2/6) * [a] + 1/2 * [a]^2 R4 = I + (1-a2/6) * [a] + (1/2-a2/24) * [a]^2
Hier gibt es klar einen Performance/Genauigkeits-Zielkonflikt. Ist die Abtastrate hoch genug und dementsprechend die Drehwinkel klein, reicht wahrscheinlich die Näherung 2. Ordnung; denn es gibt ja auch noch das Messrauschen, was ggf einen viel stärkeren Einfluss auf die Genauigkeit hat als die Approximationsfehler der Rodriguesformel.
Die verschiedenen Genauigkeiten dieser Approximationen lassen sich als verschiedene Näherung eines Kreisbogens darstellen. Siehe Bild rechts. Der Punkt rechts unten im Bild (1;0) ist der 0°-Punkt, in dem sich alle Formeln einig sind. Mit steigendem Winkel gehen sie dann auseinander.
Ideen/Strategien/TODO
- Mal so ein Rauschsignal der versch. Sensoren "richtig" angucken (Leistungsdichtespektrum)
- Temperaturabhängigkeit checken
- Wie lassen sich die Messfehler modellieren? (nur Offset und Rauschen oder auch nichtlinear?)
- überlegen, wie man sowas kalibriert
- Die Orientierung sollte sich dank Erdanziehungskraft wenigstens ein bisschen korrigieren lassen, so dass oben/unten immer noch oben/unten bleibt -- vielleicht per Complementary Filter.
- Vielleicht kann man einen Fußgänger-Modus einführen, der die Schritte per auf/ab erkennt und damit die Geschwindigkeit besser ratet, als man die über die Accelerometer integrieren kann. Als Fußgänger wird es wahrscheinlich noch besser funktionieren, wenn man sich die Sensoren auf den Schuh klebt. Damit könnte man den Drift der integrierten Geschwindigkeit elemenieren, weil man ja weiß, dass sich der Fuß relativ zum Boden in bestimmten Phasen nicht bewegt. Das nennt man "Zero Velocity Update" oder auch kurz "ZUPT".